Setting up python environment

# reset all previously defined varibles
%reset -f

# import everything from sympy moduleb 
from sympy import *

# pretty math formatting
init_printing()   # latex

Symbolic variables must be declared

x,y,z = symbols('x y z')
t     = symbols('t')

Example

Evaluate the line integral $\int_C y \, ds$ along the parabola $y = 2\sqrt{x}$ from $A(3,2\sqrt{3})$ to $B (24, 4\sqrt{6})$.

x = t
y = 2*sqrt(t)

f = y  

s = sqrt( diff(x,t)**2 + diff(y,t)**2 )

# integration
integrate(f*s,[t,3,24])

Example

Find the work done by the vector field $\mathbf{F} = r^2 \mathbf{i}$ in moving a particle along the helix $x = \cos{t}, y = \sin{t}, z = t$ from the point $(1,0,0)$ to $(1,0,4 \pi)$.

Note: $r^2 = x^2 + y^2 + z^2$

x = cos(t)
y = sin(t)
z = t

F = [x**2 + y**2 + z**2  , 0   , 0]

integrate(
          F[0]*diff(x,t) + F[1]*diff(y,t) + F[2]*diff(z,t),
          [t,0,4*pi]
         )

Example

Evaluate $\displaystyle \int_A^B 2xy\,dx + (x^2 - y^2)\, dy$ along the arc of the circle $x^2 + y^2 = 1$ in the first quadrant from $A(1,0)$ to $B(1,0)$.

x = cos(t)
y = sin(t)

F = [2*x*y, x**2 - y**2]

integrate(
          F[0]*diff(x,t) + F[1]*diff(y,t),
          [t,0,pi/2]
         )

Example

Prove that $\displaystyle \mathbf{F} = (y^2 \cos{x} + z^3)\mathbf{i} + (2y \sin{x} - 4)\mathbf{j} +(3xz^2 + z) \mathbf{k}$ is a conservative force field. Hence find the work done in moving an object in this field from point $(0,1,-1)$ to $(\pi/2, -1, 2)$.

Note:

If a vector field $\mathbf{F} = F_1 \mathbf{i} + F_2 \mathbf{j} + F_3 \mathbf{k }$ is conservative then

# reset variables from previous examples
x,y,z = symbols('x y z') 

def curl(F):
    c1 = diff(F[2],y) - diff(F[1],z)
    c2 = diff(F[0],z) - diff(F[2],x)
    c3 = diff(F[1],x) - diff(F[0],y)
    return [c1,c2,c3]

F = [(y**2 *cos(x) + z**3), 2*y* sin(x) - 4. , 3*x*z**2 + z ]

curl(F)

Zero curl implies conservative vector field.

Example

Evaluate $\underset{R}{ \int\!\!\!\!\int} (x^2 + y^2) \, dA$ over the triangle with vertices $(0,0)$, $(2,0)$, and $(1,1)$.

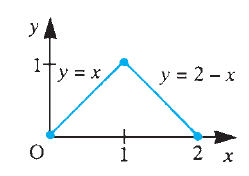
x,y = symbols('x y')

integrate( 
    integrate(x**2 + y**2, [x,y,2-y]),
    [y,0,1])

Example

Evaluate

$\underset{R}{ \int \!\!\! \int} (x + 2y )^{-1/2} \, dA$ over the region $x - 2y \le 1$ and $x \ge y^2 +1$.

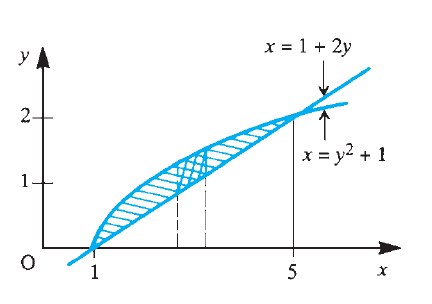
x,y = symbols('x y')


# does not work in one shot
integrate((x + 2*y)**(-Rational(1,2)), [x, y**2+1, 1+2*y])

#manually simlipy one radical

integrate(2*sqrt(4*y + 1) - 2*(y+1),[y,0,2])