How the law of conservation of heat transforms into a partial differential equation.

$$\rho c \frac{\p T}{\p t} - \nl \cdot (k \nl T) = Q + h(T_{\textrm{ext}} - T)$$

Law of conservation of Energy

For any isolated environment, rate of change of energy is equal to rate at which energy is produced inside the region, plus the rate at which energy is flowing in from environment.

Fourier’s Law

Heat flux density, $\vec{q}$, is equal to $- k \nl T$.

Heat Equation

$$\rho c \frac{\p T}{\p t} - \nl \cdot (k \nl T) = Q$$

where

$\rho$	:	density	mass per unit volume
$c$	:	specific heat	heat per unit mass per unit temperature
$c$	:	heat diffusion coefficient	material property
Q	:	heat source	per unit volume

Derivation

Let $V$ be any arbitrary volume, and $\p V$ be its boundary. Then this law is

$$\begin{array}{rcl} \textrm{rate of change of heat inside } V &=& \textrm{ rate at which heat is produced inside } V \\ & &+ \textrm{rate at which heat is flowing in } V \textrm{ through } \p V. \end{array}$$

Heat inside body an infinitesimal volume $dV$ is $c \rho T \mathrm{d}V$. We get the total volume by integrating this formula:

$$\int_V c \rho T \, \mathrm{d} V$$

Heat conservation law applied to the hypothetical volume $V$ becomes

$$\frac{d}{d t}\int_V c \rho T \, d V = \int_V Q \, d V + \int_{\p V} \vec{q}\cdot (- \hat{n})\, dA$$

Interchanging derivatives and integration on the left hand side term, and using divergence theorem on the second term on the right hand side we get

$$\int_V c \rho \frac{\p T}{\p t} \, d V = \int_V Q \, d V - \int_{V} \divc ( \vec{q}) \,dV$$

Using Fourier law on the right hand side term we get

$$\int_V c \rho \frac{\p T}{\p t} \, d V = \int_V Q \, d V + \int_{V} \divc ( k \nl T \,dV$$

Because this relation must hold for all $V$, it can be proved that (under “appropriate conditions”)

$$c \rho \frac{\p T}{\p t} - \nl \cdot (k \nl T) = Q$$

Examples

For every problem below, try to explain connect the mathematical equations with background physics in term of heat, temperature, insulation, source, etc. Then solve them on matlab and study the solutions. Don’t move onto new problem till you have a fair understanding of physics and maths connection for each problem.

Example 1

Solve the following equation on the rectangular region: ABCD, where AB = CD = 1, and AD = BC = 0.1. We are looking for the temperature function $T = T(x,y,t)$ which satisfies the equation

$$c \rho \frac{\p T}{\p t} - \divc (k \nl T) = 0,$$

where $c = 1$, $k = 0.01$. Boundary conditions are like $u = 0$ on AD and BC. Other boundaries are insulated (zero Neumann boundary condition). In addition, $u$ satisfies the initial condition $u(x,y,0) = \sin (\pi x)$.

Example 2

Consider a 1m x 0.1m two dimensional aluminium plate. Specific heat $c = 9 \times 10^{-4}$J/kg K, density $\rho 2700$ kg/$m^3$ ). You can consider the thickness of the plate to be 0.5 cm.

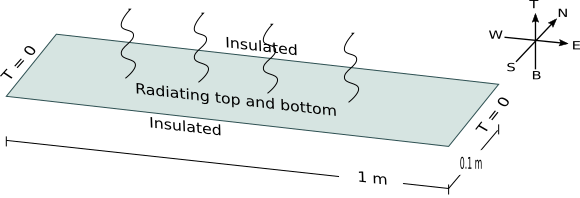
The north and south side of the plate are insulated, the east and west sides are fixed at $T = 0$ for all time. The top and bottom side of the plate are in exposed to environment, and plate and environment are regularly exchanging heat at a rate which is proportional to the difference in plate temperature and environment temperature.

Derive an equation for $T(x,y,t)$ : temperature at point $(x,y)$ at time $t$. Then solve in matlab various choices of environment temperature with initial condition $T(x,y,0) = \sin (\pi x)$.

Example 3 : Heating a plate with stove

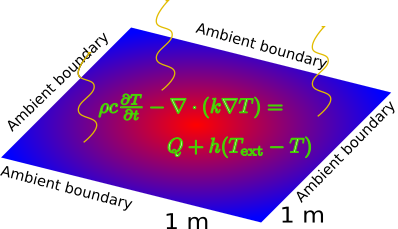
Simulate the situation described in the above figure with $Q = 50\exp \left(\frac{1}{1 + x^2 + y^2}\right)$ and appropriate choice of $\rho, c, k, h, T_{ext}$s. Try to give some physical analogy of the source term $Q$.

Example 4 : Heat sink problem

coming shortly

Example 5 : A 3d problem

coming shortly